Sistemas de Numeração
Conjunto de símbolos utilizados para representação de quantidades e de regras que definem a forma de apresentação. Cada sistema de numeração é apenas um método diferente para representar quantidades.
As quantidades em si não mudam, apenas a forma de representá-las
| Sistema | Base | Algarismos |
|---|---|---|
| Binário | 2 | 0, 1 |
| Octal | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| Decimal | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Hexadecimal | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Tabela Comparativa
| Decimal | Binário | Octal | Hexadecimal |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Conversão entre Sistemas de Numeração
Decimal para qualquer Base Númerica:
Para realizar a conversão de decimal para binário, realiza-se a divisão sucessiva pela base de destino (por exemplo, se for para hexadecimal, deve-se dividir por 16). O resultado da conversão será dado pelo último quociente (MSB) e o agrupamento dos restos de divisão será o número na base de destino.
Por exemplo, vamos converter o número 45 em binário:

A leitura do resultado é feita do último quociente para o primeiro resto. Sendo assim, o resultado da conversão do número 45 para binário é: 101101(2).
Agora, vamos converter o número 10024 para hexadecimal:

Qualquer Base Numérica para Decimal:
Nesse caso, deve-se utilizar notação polinomial.

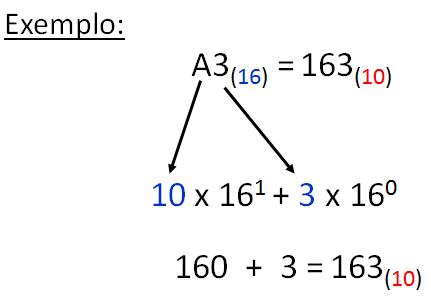
Por exemplo, vamos converter o número A3 (em hexadecimal) para decimal:
Octal/Hexadecimal para Binário (e vice-versa):
Deve-se utilizar a técnica de agrupamento de bits, associando 3 ou 4 bits a cada algarismo de octal ou hexadecimal, respectivamente.
Como exemplo, vamos converter 21, em octal e em hexadecimal, para binário:

A seguir, vamos converter 001000110 de binário para octal e hexadecimal:

Octal para Hexadecimal (e vice-versa):
Nesse caso, a conversão não é realizada diretamente e requer o uso de uma base intermediária (base binária). Para esse tipo de conversão, é necessário seguir dois passos:
- Converter o número da base original (octal ou hexadecimal) para binário.
- Converter o resultado binário para a base destino (hexadecimal ou octal).
Por exemplo, vamos converter 175 em octal para hexadecimal:
(175) 8 = (?) 16
(175) 8 = (1111101) 2 = (7D) 16